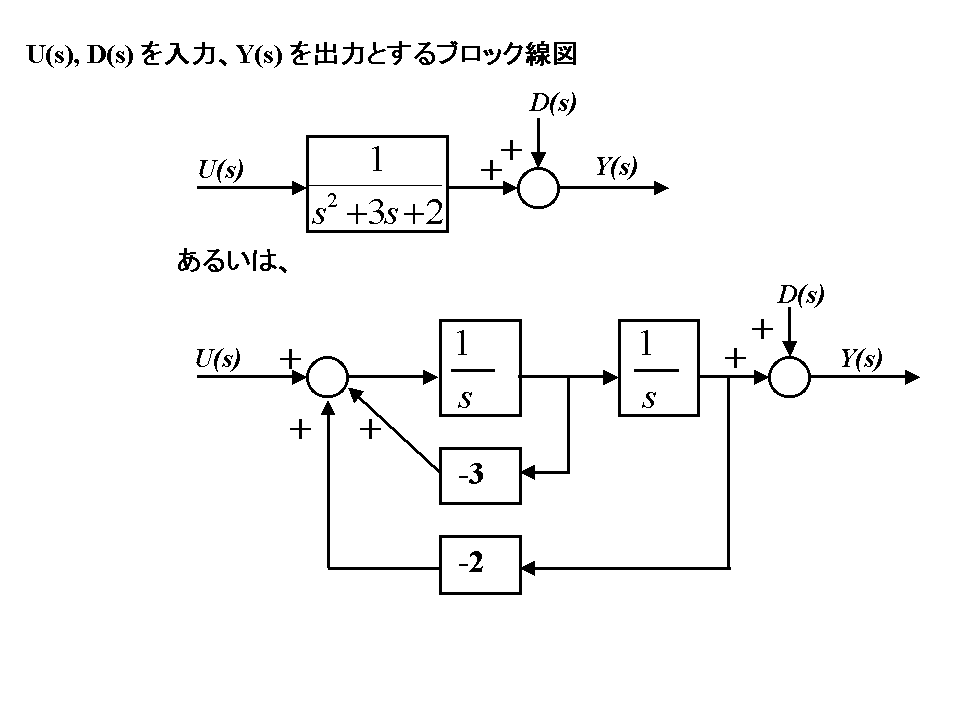
各々の式を以下のようにラプラス変換する。
dx1(t)/dt = x2(t)                              （ラプラス変換） ⇒　　s･X1(s) - x1(0) = X2(s), 　　　　　　　　　　　　　（ x1(0)=0 より）⇒　　s･X1(s) = X2(s)　　　　　　　　　　　　 　・・・（１）
dx2(t)/dt = -2･x1(t) - 3･x2(t) + u(t)  （ラプラス変換） ⇒　　s･X2(s) - x2(0) = -2･X1(s) - 3･X2(s) + U(s),　　（ x2(0)=0 より）⇒　　s･X2(s) = -2･X1(s) - 3･X2(s) + U(s),　・・・（２）
y(t) = x1(t) + d(t)                            （ラプラス変換） ⇒　　Y(s) = X1(s) + D(s),　　　　　　　・・・（３）

式（１）（２）（３）から、変数X1(s),X2(s)　を含まない式を導く。式（１）より、 X2(s) = s･X1(s) 、これを、式（２）へ代入して次を得る。
 s･s･X1(s) = -2･X1(s) - 3･s･X1(s) + U(s),   これを X1(s) について整理すると、　　(s² + 3･s + 2)X1(s) = U(s),    となる。
この式から、X1(s)　を求め　式（３）へ代入する。　　　　　Y(s) = U(s)/(s² + 3･s + 2) + D(s),           ・・・（４）　　　　　この式（４）より、各伝達関数は以下となる。

　Y(s)              1                 Y(s)
  ── = ────── ,      ── =  1,
  U(s)      s² + 3･s + 2          D(s)

問題２の（２）の解答

式（１）（２）（３）を使ってそのままブロック線図にしてもよいし、式（４）だけからブロック線図にしてもよい。その他、等価な表現方法はいくつも考えられる。

問題２の（３）の解答

d(t) = 0   for  ∀ｔ、　より、D(s) = 0, であるから、式（３）は、　Y(s) = X1(s) 　となり、　式（４）は、Y(s) = U(s)/(s² + 3･s + 2)　となる。
一方、u(t) は単位ステップ関数であるから、そのラプラス変換は　U(s) = 1/s　である。
よって、　Y(s) = (1/s)/(s² + 3･s + 2)　　となり、これをラプラス逆変換して　y(t)　を以下のように得る。
                    1             1                      1          1           1          1              e^-2t
  　y(t) = L^-1[ ─ ･ ──────] =  L^-1[──  - ──  + ───]  = ─ - e^-t + ──
                    s      s² + 3･s + 2              2s       s+1       2(s+2)       2              2
 　y(∞) = 1/2
 

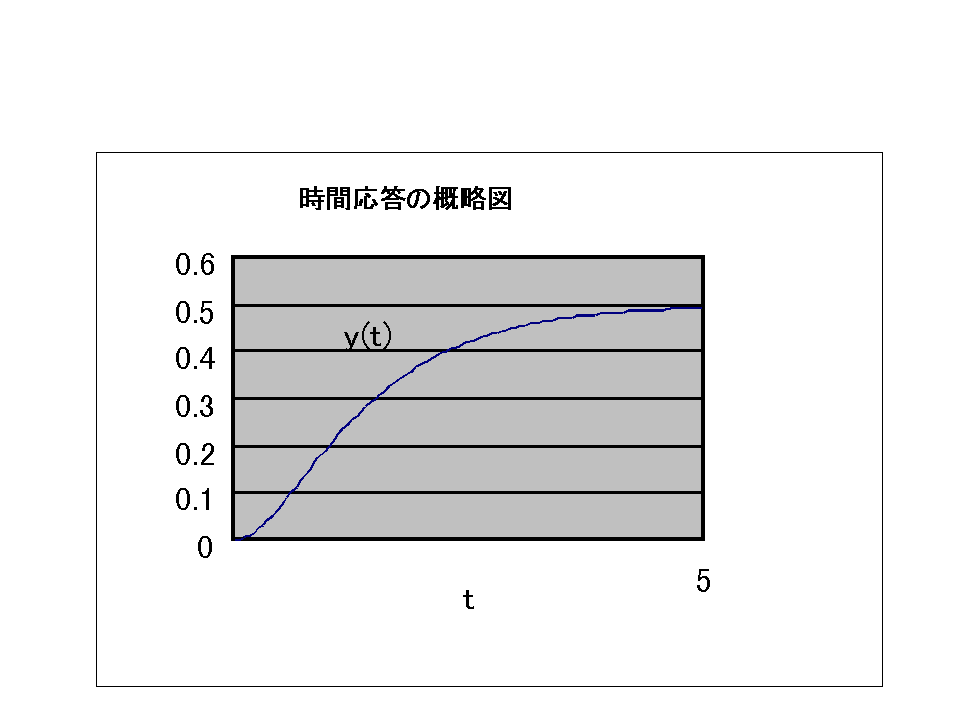
y(t)　の概略図（以下）を書くポイント。数値計算をしなくても、 初期条件  x1(0)=0, x2(0)=0,  より、
t=0 における、y および y の傾きは ０ であることが分かる。また、y(∞) = 1/2 である。

 

この問題を通して修得して欲しいポイントは、

• ラプラス変換を用いた常微分方程式の解法
• 伝達関数の分母多項式＝０とおいた式（特性方程式）の根と出力（解）の時間応答の関係（根の実部が負ならば、出力は０に収束する、根の実部が正ならば出力は無限大へ発散、根の虚数部が０でないときは、出力は振動成分を有する）

自信を持てない人は、第三講の要旨と内容を再度読み直してみて下さい。
質問のある方は、m-adachi@02.246.ne.jp  まで、メールして下さい。