PID制御と二自由度制御のシミュレーション

　　一次遅れ系とむだ時間系が直列に接続されたシステムに対して、制御を行う問題を考えよう。

（注）　PID制御のP、I、Dは、比例、積分、微分を表す英語の頭文字を取ったものである。
        PID制御のパラメータ（K_P、T_I、 T_D）を決めるには、ステップ応答のむだ時間や立ち上がり速度情報を用いる方法や周波数入力に対する応答から決める方法など、経験的な方法があり、
PID制御の基礎と応用、山本重彦・加藤尚武著、朝倉書店（１９９７年刊）、
PID制御、須田信英著、朝倉書店（１９９２年刊）、
等に詳しく書かれているので、ここでは省略する。以下で用いるパラメータの値は、これらの経験的方法で推奨されているものである。

   ここでは、次のような３つのケースについてシミュレーションを行うこととする。

１）　目標関数r(t)=0, for ∀t 、単位ステップ関数状の外乱が存在する場合に、 PID制御（K_P=6.3、 T_I=0.4、T_D=0.08）、あるいは、
　　　二自由度制御（K_P=6.3、T_I=0.4、T_D=0.08、 α=0.61、β=0.64）を行った時の出力 y(t) の応答を求める。
(注）この場合の目標r(t)は常に零なので、二自由度制御とPID制御は、同じ応答を示す。
      PID制御のパラメータ（K_P=6.3、 T_I=0.4、T_D=0.08）は、ステップ外乱に対する出力応答より決められた値である。

２）　外乱が無く（ d(t)=0）、目標関数が単位ステップ関数である場合において、
　　　PID制御（K_P=6.3、T_I=0.4、T_D=0.08）のみを行った時の出力 y(t) の応答を求める。

３）　外乱が無く（ d(t)=0）、目標関数が単位ステップ関数である場合において、
　　　二自由度制御（K_P=6.3、T_I=0.4、T_D=0.08、 α=0.61、β=0.64）を行った時の出力 y(t) の応答を求める。

（注）　現在の時刻までの偏差情報から、現在の時刻の偏差の微分値は計算できないことに注意する必要がある。したがって、偏差の微分をT_D倍する値を計算する式は、通常以下のような近似式で代用される。
      u_d(t)=T_D･(de(t)/dt) と置くとき、　　u_d(t)+ 0.01･(du_d(t)/dt)=T_D･(de(t)/dt)

ケース１の場合のシミュレーションソフトは、以下であり、応答波形、操作量として次のグラフを得られる。

Sub PID1()

   Dim r(1001) As Double, d(1001) As Double, y(1001) As Double, x(1001) As Double
   Dim drdt(1001) As Double
   Dim dydt(1001) As Double
   Dim e(1001) As Double, ie(1001) As Double, iud(1001) As Double
   Dim dedt(1001) As Double
   Dim time(1001) As Double, dt As Double
   Dim u(1001) As Double, up(1001) As Double, ui(1001) As Double, ud(1001) As Double
   Dim kp As Double, ti As Double, td As Double

   Set WS = Worksheets("Sheet1")
   WS.Activate
   Range("A1:M1300").Select
   Selection.Clear

    Cells(1, 1) = "時刻 t(sec)"
    Cells(2, 2) = "目標値r(t)"
    Cells(2, 3) = "出力y(t)"
    Cells(2, 4) = "内部状態x(t)"

    Cells(1, 5) = "時刻 t(sec)"
    Cells(2, 6) = "操作量u(t)"
    Cells(2, 7) = "比例要素成分up(t)"
    Cells(2, 8) = "積分要素成分ui(t)"
    Cells(2, 9) = "微分要素成分ud(t)"

' 開始時刻を０とする
time(0) = 0
' 時間積分の間隔を0.0025秒とする
dt = 0.0025

' PID制御のパラメータ
kp = 6.3
ti = 0.4
td = 0.08
' 初期値
          y(0) = 0
          r(0) = 0
          dydt(0) = 0
          up(0) = 0
          ui(0) = 0
          ud(0) = 0
          u(0) = 0
          e(0) = r(0) - y(0)
          ie(0) = 0
          iud(0) = 0
'　目標関数　r(t)=1, for t>0, 　より、
For i = 0 To 1000
time(i) = dt * i
r(i) = 0
d(i) = 1
Next
' 初期条件：x(0) = 0 for t≦0　より、
x(0) = 0

'目標値応答
For i = 1 To 80
y(i) = 0
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
u(i) = up(i) + ui(i) + ud(i)
x(i) = x(i - 1) + (u(i - 1) + d(i - 1) - x(i - 1)) * dt
Next

For i = 81 To 1000
y(i) = x(i - 80)
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
u(i) = up(i) + ui(i) + ud(i)
x(i) = x(i - 1) + (u(i - 1) + d(i - 1) - x(i - 1)) * dt
Next

' グラフ出力用データのSheet1への書き込み
For i = 0 To 1000
          Cells(i + 3, 1) = time(i)
          Cells(i + 3, 2) = r(i)
          Cells(i + 3, 3) = y(i)
          Cells(i + 3, 4) = x(i)
          Cells(i + 3, 5) = time(i)
          Cells(i + 3, 6) = u(i)
          Cells(i + 3, 7) = up(i)
          Cells(i + 3, 8) = ui(i)
          Cells(i + 3, 9) = ud(i)
          Cells(i + 3, 10) = time(i)
Next

    Range("A2:D703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet1").Range("A2:D703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet1"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "PID制御における外乱応答波形"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

    Range("E2:I703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet1").Range("E2:I703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet1"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "ステップ外乱におけるPID制御操作量"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

End Sub

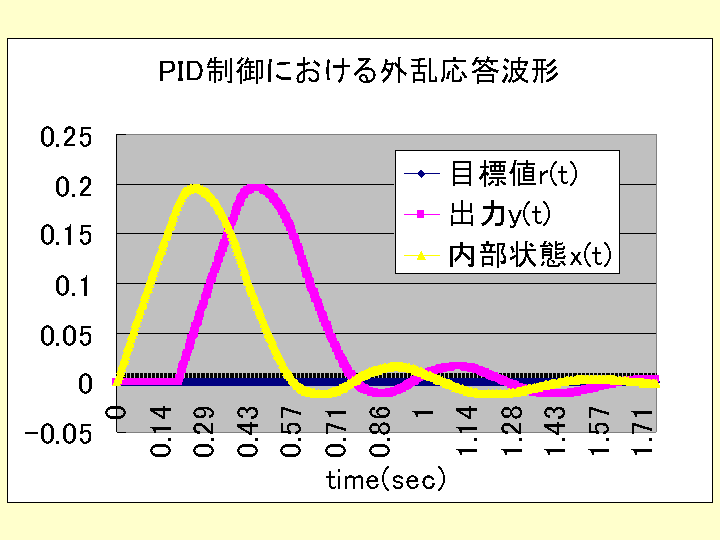
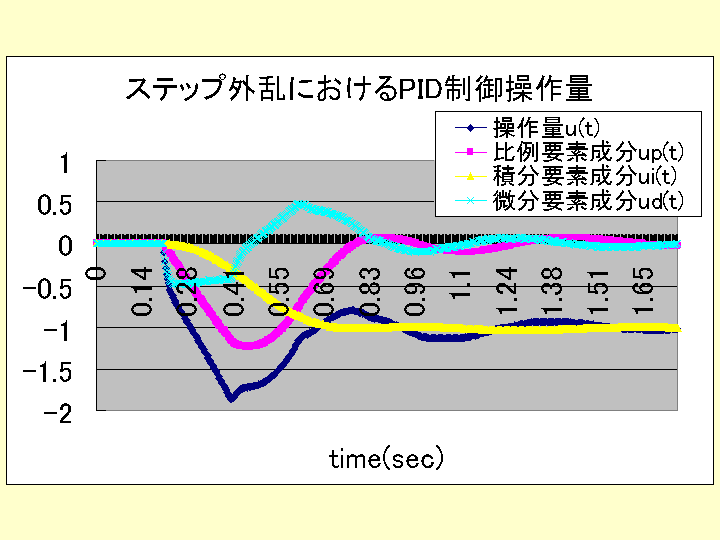
ただし、up(t),ui(t),ud(t) とは、u(t)=up(t)+ui(t)+ud(t)　の内の偏差の比例、積分、微分から求められる成分を表している。

ケース２の場合のシミュレーションソフトは、以下であり、応答波形、操作量として次のグラフを得られる。

Sub PID2()

   Dim r(1001) As Double, d(1001) As Double, y(1001) As Double, x(1001) As Double
   Dim drdt(1001) As Double
   Dim dydt(1001) As Double
   Dim e(1001) As Double, ie(1001) As Double, iud(1001) As Double
   Dim dedt(1001) As Double
   Dim time(1001) As Double, dt As Double
   Dim u(1001) As Double, up(1001) As Double, ui(1001) As Double, ud(1001) As Double
   Dim kp As Double, ti As Double, td As Double

   Set WS = Worksheets("Sheet2")
   WS.Activate
   Range("A1:M1300").Select
   Selection.Clear

    Cells(1, 1) = "時刻 t(sec)"
    Cells(2, 2) = "目標値r(t)"
    Cells(2, 3) = "出力y(t)"
    Cells(2, 4) = "内部状態x(t)"

    Cells(1, 5) = "時刻 t(sec)"
    Cells(2, 6) = "操作量u(t)"
    Cells(2, 7) = "比例要素成分up(t)"
    Cells(2, 8) = "積分要素成分ui(t)"
    Cells(2, 9) = "微分要素成分ud(t)"

' 開始時刻を０とする
time(0) = 0
' 時間積分の間隔を0.0025秒とする
dt = 0.0025

' PID制御のパラメータ
kp = 6.3
ti = 0.4
td = 0.08
' 初期値
          y(0) = 0
          r(0) = 0
          dydt(0) = 0
          up(0) = 0
          ui(0) = 0
          ud(0) = 0
          u(0) = 0
          e(0) = r(0) - y(0)
          ie(0) = 0
          iud(0) = 0
'　目標関数　r(t)=1, for t>0, 　より、
For i = 0 To 1000
time(i) = dt * i
          If i < 10 Then
          r(i) = 0.1 * (i + 1)
          Else
          r(i) = 1
          End If
Next
' 初期条件：x(0) = 0 for t≦0　より、
x(0) = 0

'目標値応答
For i = 1 To 80
y(i) = 0
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
u(i) = up(i) + ui(i) + ud(i)
x(i) = x(i - 1) + (u(i - 1) - x(i - 1)) * dt
Next

For i = 81 To 1000
y(i) = x(i - 80)
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
u(i) = up(i) + ui(i) + ud(i)
x(i) = x(i - 1) + (u(i - 1) - x(i - 1)) * dt
Next

For i = 0 To 1000
          Cells(i + 3, 1) = time(i)
          Cells(i + 3, 2) = r(i)
          Cells(i + 3, 3) = y(i)
          Cells(i + 3, 4) = x(i)
          Cells(i + 3, 5) = time(i)
          Cells(i + 3, 6) = u(i)
          Cells(i + 3, 7) = up(i)
          Cells(i + 3, 8) = ui(i)
          Cells(i + 3, 9) = ud(i)
          Cells(i + 3, 10) = time(i)
Next

    Range("A2:D703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet2").Range("A2:D703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet2"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "ステップ目標におけるPID制御の応答波形"
'        .HasTitle = False
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

    Range("E2:I703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet2").Range("E2:I703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet2"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "ステップ目標におけるPID制御操作量"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

End Sub

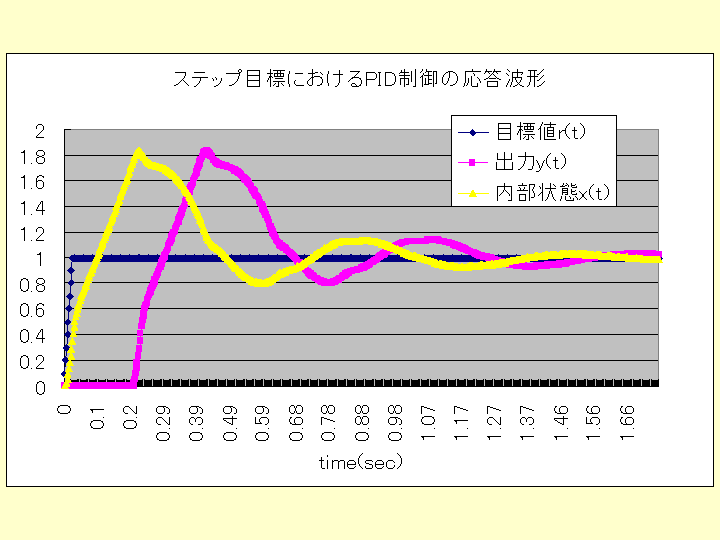
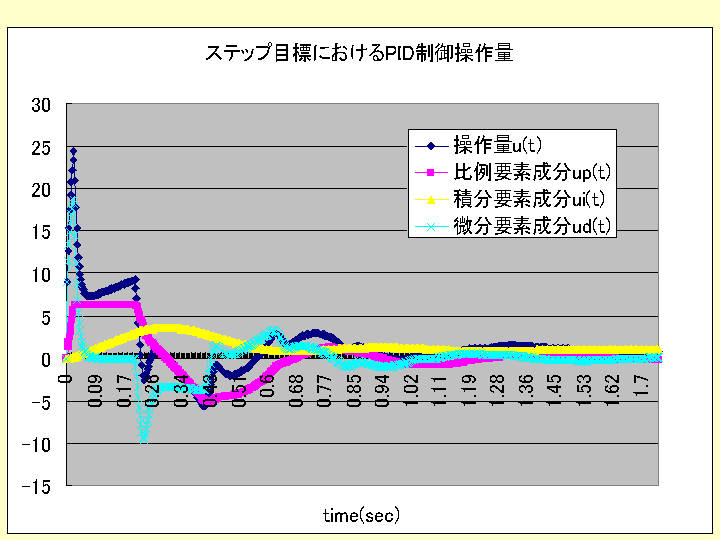
（注）　上記シミュレーションソフトにおいて、PID制御のパラメータ（K_P、 T_I、T_D）の各値をそれぞれ単独に増減させたシミュレーションをやることにより、比例要素、積分要素、微分要素の働きを知ることができます。

ケース３の場合のシミュレーションソフトは、以下であり、応答波形、操作量として次のグラフを得られる。

Sub PID3()

   Dim r(1001) As Double, d(1001) As Double, y(1001) As Double, x(1001) As Double
   Dim drdt(1001) As Double
   Dim dydt(1001) As Double
   Dim e(1001) As Double, ie(1001) As Double, iud(1001) As Double
   Dim dedt(1001) As Double
   Dim time(1001) As Double, dt As Double
   Dim up(1001) As Double, ui(1001) As Double, ud(1001) As Double
   Dim upf(1001) As Double, udf(1001) As Double
   Dim kp As Double, ti As Double, td As Double
   Dim alpha As Double, beta As Double
   Dim u(1001) As Double, uff(1001) As Double, ufb(1001) As Double

   Set WS = Worksheets("Sheet3")
   WS.Activate
   Range("A1:M1300").Select
   Selection.Clear

    Cells(1, 1) = "時刻 t(sec)"
    Cells(2, 2) = "目標値r(t)"
    Cells(2, 3) = "出力y(t)"
    Cells(2, 4) = "内部状態x(t)"

    Cells(1, 5) = "時刻 t(sec)"
    Cells(2, 6) = "fb操作量ufb(t)"
    Cells(2, 7) = "比例要素成分up(t)"
    Cells(2, 8) = "積分要素成分ui(t)"
    Cells(2, 9) = "微分要素成分ud(t)"

    Cells(1, 10) = "時刻 t(sec)"
    Cells(2, 11) = "操作量u(t)"
    Cells(2, 12) = "ff成分uff(t)"
    Cells(2, 13) = "fb成分ufb(t)"

    Cells(2, 16) = "ff操作量uff(t)"
    Cells(2, 17) = "比例要素成分upf(t)"
    Cells(2, 18) = "微分要素成分udf(t)"

' 開始時刻を０とする
time(0) = 0
' 時間積分の間隔を0.0025秒とする
dt = 0.0025

' 二自由制御のパラメータ
kp = 6.3
ti = 0.4
td = 0.08
alpha = 0.61
beta = 0.64

' 初期値
          y(0) = 0
          r(0) = 0
          dydt(0) = 0
          up(0) = 0
          ui(0) = 0
          ud(0) = 0
          u(0) = 0
          e(0) = r(0) - y(0)
          ie(0) = 0
          iud(0) = 0
'　目標関数　r(t)=1, for t>0, 　より、
For i = 0 To 1000
time(i) = dt * i
          If i < 10 Then
          r(i) = 0.1 * (i + 1)
          Else
          r(i) = 1
          End If
Next
' 初期条件：x(0) = 0 for t≦0　より、
x(0) = 0

'目標値応答
For i = 1 To 80
y(i) = 0
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
ufb(i) = up(i) + ui(i) + ud(i)
upf(i) = -kp * alpha * r(i - 1)
udf(i) = (-kp * td * beta * 100 * (r(i) - r(i - 1)) + (1 - 100 * dt / 2) * udf(i - 1)) / (1 + 100 * dt / 2)
uff(i) = upf(i) + udf(i)
u(i) = uff(i) + ufb(i)
x(i) = x(i - 1) + (u(i - 1) - x(i - 1)) * dt
Next

For i = 81 To 1000
y(i) = x(i - 80)
e(i) = r(i) - y(i)
ie(i) = e(i - 1) * dt + ie(i - 1)
iud(i) = ud(i - 1) * dt + iud(i - 1)
up(i) = kp * e(i - 1)
ui(i) = kp * ie(i - 1) / ti
ud(i) = (kp * td * 100 * (e(i) - e(i - 1)) + (1 - 100 * dt / 2) * ud(i - 1)) / (1 + 100 * dt / 2)
ufb(i) = up(i) + ui(i) + ud(i)
upf(i) = -kp * alpha * r(i - 1)
udf(i) = (-kp * td * beta * 100 * (r(i) - r(i - 1)) + (1 - 100 * dt / 2) * udf(i - 1)) / (1 + 100 * dt / 2)
uff(i) = upf(i) + udf(i)
u(i) = uff(i) + ufb(i)
x(i) = x(i - 1) + (u(i - 1) - x(i - 1)) * dt
Next

' グラフ出力用データのSheet1への書き込み
For i = 0 To 1000
          Cells(i + 3, 1) = time(i)
          Cells(i + 3, 2) = r(i)
          Cells(i + 3, 3) = y(i)
          Cells(i + 3, 4) = x(i)
          Cells(i + 3, 5) = time(i)
          Cells(i + 3, 6) = u(i)
          Cells(i + 3, 7) = up(i)
          Cells(i + 3, 8) = ui(i)
          Cells(i + 3, 9) = ud(i)
          Cells(i + 3, 10) = time(i)
          Cells(i + 3, 11) = u(i)
          Cells(i + 3, 12) = uff(i)
          Cells(i + 3, 13) = ufb(i)
          Cells(i + 3, 16) = uff(i)
          Cells(i + 3, 17) = upf(i)
          Cells(i + 3, 18) = udf(i)
Next

    Range("A2:D703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet3").Range("A2:D703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet3"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "ステップ目標における二自由度制御の応答波形"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

    Range("J2:M703").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet3").Range("J2:M703"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet3"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "ステップ目標における二自由度制御操作量"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = False
    End With

End Sub

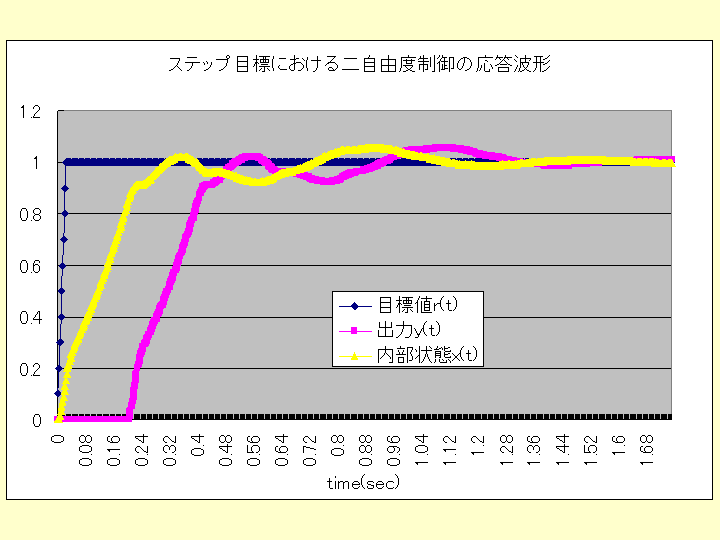
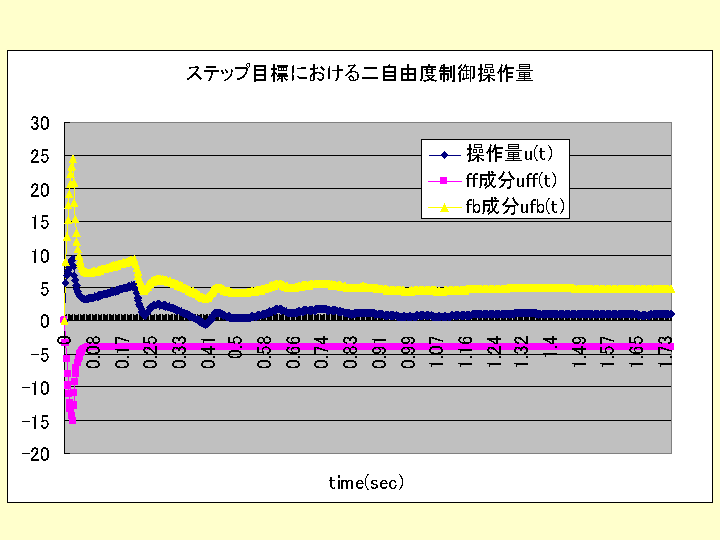
ただし、uff(t),ufb(t) とは、u(t)=uff(t)+ufb(t)　の内の目標のフィードフォワード、偏差のフィードバックから求められる成分を表している。

以上の３ケースのシミュレーション結果から、外乱応答に対して乱れが少なく、ステップ状の目標値へ変更に対してすばやく、オオバーシュートも少なく、操作量の絶対値も少なくてすむ（これは、アクチュエータの能力が低くてもよいことを意味している）のは、二自由度制御の方であることが分かる。

（注）　m-adachi@02.246.ne.jp へメールで依頼があれば、上記エクセルのソフトをメールの添付ファイルで送ります。