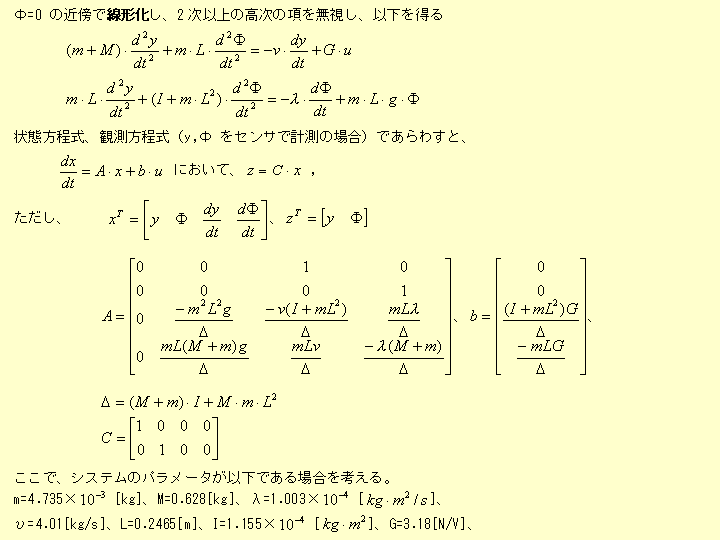倒立振子のシミュレーション２

　　ここでは、レギュレーション制御（振子が倒立位置から傾いても、もとの倒立位置に戻す制御）を実現する制御手法
１）　状態オブザーバの出力をフィドバックする制御
２）　ファジィ制御
について紹介する。

１）　状態オブザーバ利用のレギュレーション
　　振子が倒立位置から傾いても、もとの倒立位置に戻す制御を状態オブザーバの出力をフィードバックする制御で実現できることを、数値シミュレーションで確かめてみよう。制御対象は非線形システムであるので、オブザーバを設計するためには、もとのシステムを線形化するする必要がある。

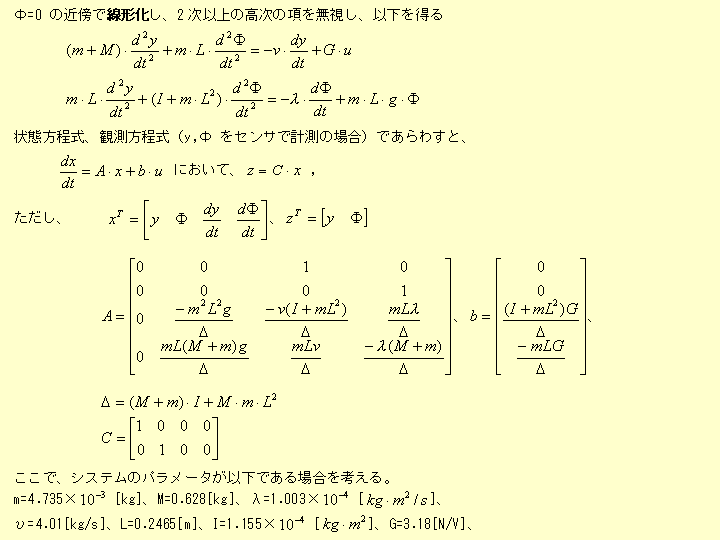
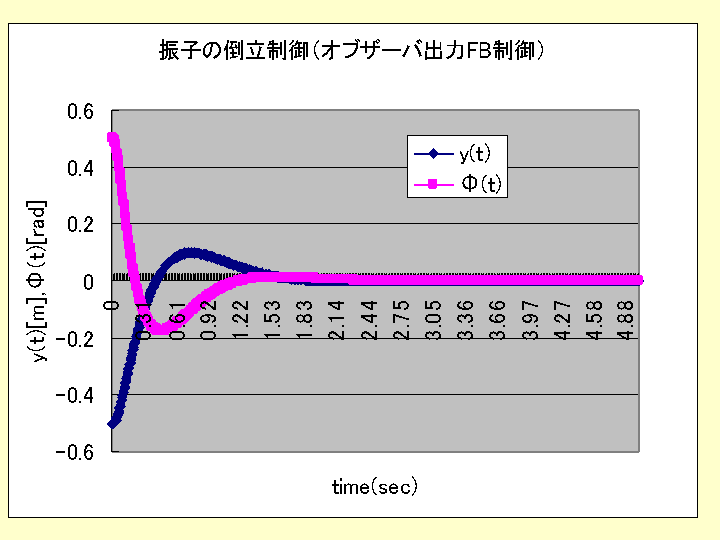
この制御則を用いて元の非線形システムを制御した場合のシミュレーション結果は以下に示すものである。
初期条件は、φ(0)=0.5[rad], dφ(0)/dt=0[rad/s], y(0)=-0.5[m], dy(0)/dt=0　　とおいている。
この結果を出すのに用いたソフトをグラフの下に示すので、初期の振子の傾き角を変更して、どの角度までなら振子をもとの垂直の位置へ戻せるのか、調べてみるのもおもしろいと思います。この限界の角度は、当然、アクチュエータのモータの能力に依存します。

Sub touritsu3()

Dim A(1 To 2, 1 To 2) As Double, Ainv(1 To 2, 1 To 2) As Double
Dim b(1 To 2, 1 To 2) As Double, dummy(1 To 2) As Double
Dim time(1001) As Double, dt As Double
Dim y(1001) As Double, dydt(1001) As Double, ddyddt(1001)
Dim phi(1001) As Double, dphidt(1001) As Double, ddphiddt(1001)
Dim u(1001) As Double
Dim mp As Double, mc As Double, lambda As Double, ny As Double
Dim leng As Double, inam As Double, ga As Double, g As Double
Dim i As Integer, j As Integer
Dim ey(1001) As Double, edydt(1001) As Double, eddyddt(1001)
Dim ephi(1001) As Double, edphidt(1001) As Double, eddphiddt(1001)
Dim f(1 To 4) As Double, k(1 To 4, 1 To 2) As Double
Dim AA(1 To 4, 1 To 4) As Double, AAkc(1 To 4, 1 To 4) As Double
Dim delta As Double, bb(1 To 4) As Double, c(1 To 2, 1 To 4) As Double
Dim dum(1 To 4) As Double

   Set WS = Worksheets("Sheet3")
   WS.Activate
   Range("A1:I1300").Select
   Selection.Clear

mp = 0.004735
mc = 0.628
lambda = 0.0001003
ny = 4.01
leng = 0.2465
inam = 0.0001155
ga = 3.18
g = 9.8

' 非線形システムの応答シミュレーション
' 差分時間     0.005
dt = 0.005
For i = 0 To 1000
time(i) = i * dt
u(i) = 0
Next
' 初期値
phi(0) = 0.5
dphidt(0) = 0
y(0) = -0.5
dydt(0) = 0
ddphiddt(0) = 0
ddyddt(0) = 0

ephi(0) = 0.5
edphidt(0) = 0
ey(0) = -0.5
edydt(0) = 0

' 近似線形システム
delta = (mp + mc) * inam + mp * mc * leng * leng
AA(1, 1) = 0
AA(1, 2) = 0
AA(1, 3) = 1
AA(1, 4) = 0
AA(2, 1) = 0
AA(2, 2) = 0
AA(2, 3) = 0
AA(2, 4) = 1
AA(3, 1) = 0
AA(3, 2) = -(mp * mp * leng * leng * g) / delta
AA(3, 3) = -ny * (inam + mp * leng * leng) / delta
AA(3, 4) = mp * leng * lambda / delta
AA(4, 1) = 0
AA(4, 2) = mp * leng * (mp + mc) * g / delta
AA(4, 3) = mp * leng * ny / delta
AA(4, 4) = -lambda * (mp + mc) / delta
bb(1) = 0
bb(2) = 0
bb(3) = (inam + mp * leng * leng) * ga / delta
bb(4) = -mp * leng * ga / delta
c(1, 1) = 1
c(1, 2) = 0
c(1, 3) = 0
c(1, 4) = 0
c(2, 1) = 0
c(2, 2) = 1
c(2, 3) = 0
c(2, 4) = 0

' フィードバックゲインf、オブザーバゲインk
f(1) = -10
f(2) = -26.2928
f(3) = -8.4844
f(4) = -4.5618

k(1, 1) = 12.9799
k(2, 1) = 11.1386
k(3, 1) = 9.4331
k(4, 1) = 158.7787
k(1, 2) = 0.2396
k(2, 2) = 22.4001
k(3, 2) = 0.9293
k(4, 2) = 154.2044

For i = 1 To 4
     For j = 1 To 4
     AAkc(i, j) = AA(i, j) - k(i, 1) * c(1, j) - k(i, 2) * c(2, j)
     Next
Next

For i = 1 To 1000
   phi(i) = phi(i - 1) + dphidt(i - 1) * dt
   y(i) = y(i - 1) + dydt(i - 1) * dt

   dphidt(i) = dphidt(i - 1) + ddphiddt(i - 1) * dt
   dydt(i) = dydt(i - 1) + ddyddt(i - 1) * dt

   A(1, 1) = mp + mc
   A(1, 2) = mp * leng * Cos(phi(i - 1))
   A(2, 1) = mp * leng * Cos(phi(i - 1))
   A(2, 2) = inam + mp * leng * leng
   Ainv(1, 1) = A(2, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 2) = A(1, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(1, 2) = -A(1, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 1) = -A(2, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))

dummy(1) = Ainv(1, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(1, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(1, 1) * ga * u(i - 1)
dummy(2) = Ainv(2, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(2, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(2, 1) * ga * u(i - 1)
ddyddt(i) = dummy(1)
ddphiddt(i) = dummy(2)

Cells(3 + i, 12) = Ainv(1, 1)
Cells(3 + i, 13) = Ainv(1, 2)
Cells(3 + i, 14) = Ainv(2, 1)
Cells(3 + i, 15) = Ainv(2, 2)

' 状態オブザーバＦＢのレギュレータ
'% オブザーバの固有値   -9 -10   -11   -12
     For j = 1 To 4
     dum(j) = AAkc(j, 1) * ey(i - 1) + AAkc(j, 2) * ephi(i - 1) + AAkc(j, 3) * edydt(i - 1) + AAkc(j, 4) * edphidt(i - 1)
     Next

ey(i) = ey(i - 1) + (dum(1) + k(1, 1) * y(i - 1) + k(1, 2) * phi(i - 1) + bb(1) * u(i - 1)) * dt
ephi(i) = ephi(i - 1) + (dum(2) + k(2, 1) * y(i - 1) + k(2, 2) * phi(i - 1) + bb(2) * u(i - 1)) * dt
edydt(i) = edydt(i - 1) + (dum(3) + k(3, 1) * y(i - 1) + k(3, 2) * phi(i - 1) + bb(3) * u(i - 1)) * dt
edphidt(i) = edphidt(i - 1) + (dum(4) + k(4, 1) * y(i - 1) + k(4, 2) * phi(i - 1) + bb(4) * u(i - 1)) * dt

u(i) = -f(1) * ey(i) - f(2) * ephi(i) - f(3) * edydt(i) - f(4) * edphidt(i)

Next

Cells(1, 2) = "時刻t(sec)"
Cells(2, 3) = "y(t)"
Cells(2, 4) = "Φ(t)"
Cells(2, 5) = "u(t)"

For i = 0 To 1000
Cells(3 + i, 2) = time(i)
Cells(3 + i, 3) = y(i)
Cells(3 + i, 4) = phi(i)
Cells(3 + i, 5) = u(i)
Next

    Range("B2:D1003").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet3").Range("B2:D1003"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet3"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "振子の倒立制御（オブザーバ出力FB制御）"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = True
        .Axes(xlValue, xlPrimary).AxisTitle.Characters.Text = "y(t)[m],Φ(t)[rad]"
    End With

End Sub

２）　ファジィ制御
　　上記のオブザーバ利用FB制御では、線形化された数式モデルに立脚して制御アルゴリズムが導かれたものである。しかし、制御対象のモデルを知らなくても人間の持つ知識に基づいて倒立制御が実現できるだろうと思われる。
人は箒を手の上で立たせることができる。このアナロジーから、次のような知識が導かれる。
ルール１’）　振子が大きく傾いており、さらに大きく傾く方向に動いているときには、立てる方向に台車を大きく動かす方向に操作量を加える。
ルール２’）　振子が小さく傾いており、さらに傾きがゼロになる方向に大きく動いているときには、オーバーシュートして逆方向に傾くことを避けるために、傾き是正と反する方向に台車を中くらい動かす方向に操作量を加える。
ルール３’）　振子が小さく傾いており、傾きの変化速度がほぼゼロならば、立てる方向に台車を動かす方向に小さく操作量を加える。
このルールを数式で表現すると、以下であり、
   If Φ is PB and dΦ/dt is P then u is PB　　（ルール１’対応）　　　・・・　これを新たにルール１と呼ぶ。
   If Φ is NB and dΦ/dt is N then u is NB　　（ルール１’対応）　　　・・・　これを新たにルール２と呼ぶ。
   If Φ is PS and dΦ/dt is NB then u is NM　　（ルール２’対応）　　　・・・　これを新たにルール３と呼ぶ。
   If Φ is NS and dΦ/dt is PB then u is PM　　（ルール２’対応）　　　・・・　これを新たにルール４と呼ぶ。
   If Φ is PS and dΦ/dt is ZO then u is PS　　（ルール３’対応）　　　・・・　これを新たにルール５と呼ぶ。
   If Φ is NS and dΦ/dt is ZO then u is NS　　（ルール３’対応）　　　・・・　これを新たにルール６と呼ぶ。
これらのルールにもとづくファジィ制御の操作量は次式で表される。
       u(t) = (10 * kar1 - 10 * kar2 - 3 * kar3 + 3 * kar4 + 1*kar5 - 1*kar6) / (dum = kar1 + kar2 + kar3 + kar4 + kar5 + kar6)
上式における、10 * kar1の１０は（u is PB）を簡易的に表したものであり、以下同様に、- 10 * kar2のー１０は（u is NB）を、- 3 * kar3のー３は（u is NM）を、3 * kar4の３は（u is PM）を、1*kar5の１は（u is PS）を、- 1*kar6のー１は（u is NS）をそれぞれ簡易に表したものである。また、kar1、からkar6は上記６個の各ルールの（Φ、 dΦ/dt )における適合度のことで、
    kar1 = min{ Φ is PBのメンバーシップ関数（Φ）、dΦ/dt is Pのメンバーシップ関数（dΦ/dt） }
    kar2 = min{ Φ is NBのメンバーシップ関数（Φ）、dΦ/dt is Nのメンバーシップ関数（dΦ/dt） }
    kar3 = min{ Φ is PSのメンバーシップ関数（Φ）、dΦ/dt is NBのメンバーシップ関数（dΦ/dt） }
    kar4 = min{ Φ is NSのメンバーシップ関数（Φ）、dΦ/dt is PBのメンバーシップ関数（dΦ/dt） }
    kar5 = min{ Φ is PSのメンバーシップ関数（Φ）、dΦ/dt is ZOのメンバーシップ関数（dΦ/dt） }
    kar6 = min{ Φ is NSのメンバーシップ関数（Φ）、dΦ/dt is ZOのメンバーシップ関数（dΦ/dt） }
で計算されるものである。各メンバーシップ関数は、以下に示すものである。

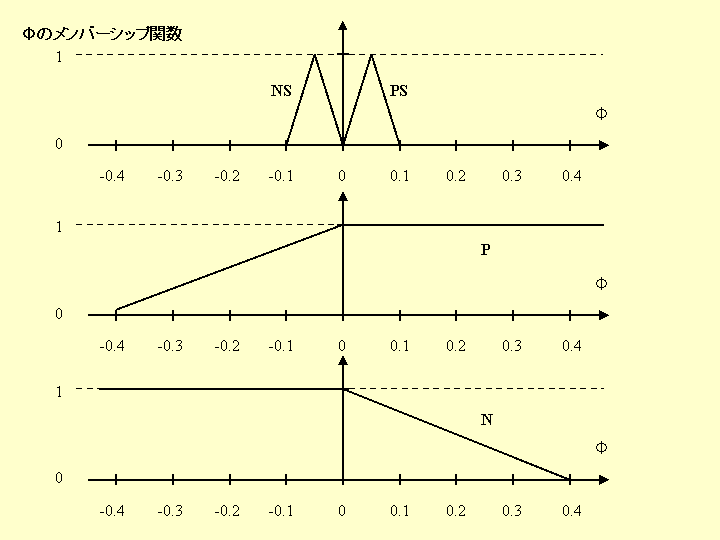
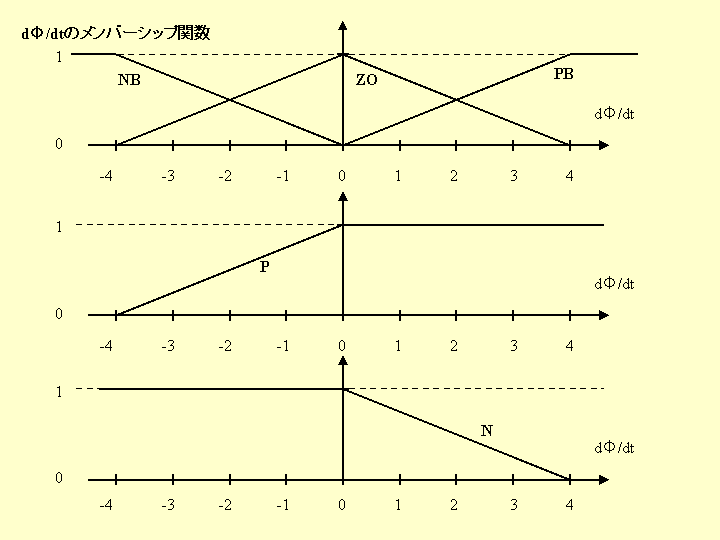
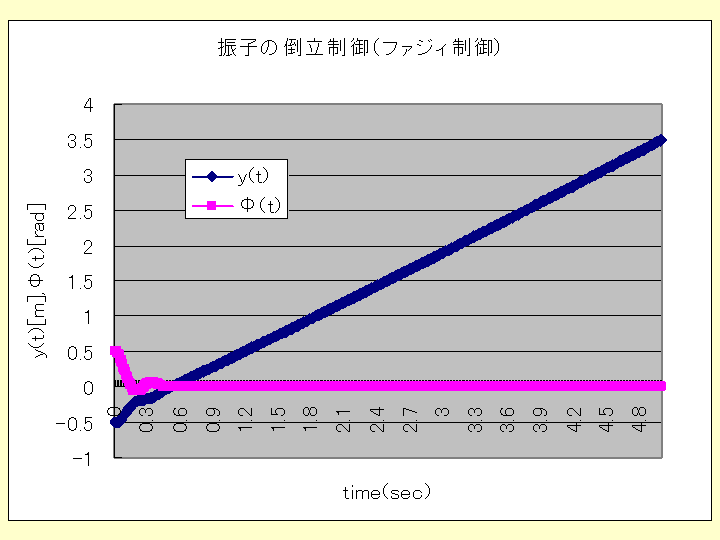
これらのファジィ制御を行ったときの応答は、以下のグラフに示すものであり、そのソフトはグラフの下に現すものである。ただし、初期条件は、φ(0)=0.5[rad], dφ(0)/dt=0[rad/s], y(0)=-0.5[m], dy(0)/dt=0　　とおいている。

Sub touritsu4()

Dim A(1 To 2, 1 To 2) As Double, Ainv(1 To 2, 1 To 2) As Double
Dim b(1 To 2, 1 To 2) As Double, dummy(1 To 2) As Double
Dim time(1001) As Double, dt As Double
Dim y(1001) As Double, dydt(1001) As Double, ddyddt(1001)
Dim phi(1001) As Double, dphidt(1001) As Double, ddphiddt(1001)
Dim u(1001) As Double
Dim mp As Double, mc As Double, lambda As Double, ny As Double
Dim leng As Double, inam As Double, ga As Double, g As Double
Dim i As Integer, j As Integer
Dim f(1 To 4) As Double

Dim kspbphi As Double, ksnbphi As Double, kszophi As Double
Dim kspdphi As Double, ksndphi As Double, kszodphi As Double
Dim dum As Double, kar1 As Double, kar2 As Double
Dim kar3 As Double, kar4 As Double, kar5 As Double, kar6 As Double
Dim kspsphi As Double, ksnsphi As Double
Dim kspbdphi As Double, ksnbdphi As Double

   Set WS = Worksheets("Sheet4")
   WS.Activate
   Range("A1:I1300").Select
   Selection.Clear

mp = 0.004735
mc = 0.628
lambda = 0.0001003
ny = 4.01
leng = 0.2465
inam = 0.0001155
ga = 3.18
g = 9.8

' 非線形システムの応答シミュレーション
' 差分時間     0.005
dt = 0.005
For i = 0 To 1000
time(i) = i * dt
u(i) = 0
Next
' 初期値
phi(0) = 0.5
dphidt(0) = 0
y(0) = -0.5
dydt(0) = 0
ddphiddt(0) = 0
ddyddt(0) = 0

For i = 1 To 1000

   phi(i) = phi(i - 1) + dphidt(i - 1) * dt
   y(i) = y(i - 1) + dydt(i - 1) * dt

   dphidt(i) = dphidt(i - 1) + ddphiddt(i - 1) * dt
   dydt(i) = dydt(i - 1) + ddyddt(i - 1) * dt

   A(1, 1) = mp + mc
   A(1, 2) = mp * leng * Cos(phi(i - 1))
   A(2, 1) = mp * leng * Cos(phi(i - 1))
   A(2, 2) = inam + mp * leng * leng
   Ainv(1, 1) = A(2, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 2) = A(1, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(1, 2) = -A(1, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 1) = -A(2, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))

dummy(1) = Ainv(1, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(1, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(1, 1) * ga * u(i - 1)
dummy(2) = Ainv(2, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(2, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(2, 1) * ga * u(i - 1)
ddyddt(i) = dummy(1)
ddphiddt(i) = dummy(2)

Cells(3 + i, 12) = Ainv(1, 1)
Cells(3 + i, 13) = Ainv(1, 2)
Cells(3 + i, 14) = Ainv(2, 1)
Cells(3 + i, 15) = Ainv(2, 2)

'    ファジィ制御
'    If Φ is PB and dΦdt is P then u is PB
'    If Φ is NB and dΦdt is N then u is NB
'    If Φ is PS and dΦdt is NB then u is NM
'    If Φ is NS and dΦdt is PB then u is PM
'    If Φ is PS and dΦdt is ZO then u is PS
'    If Φ is NS and dΦdt is ZO then u is NS

       If phi(i) > 0.4 Then
       kspbphi = 1
       ElseIf phi(i) > 0 Then
       kspbphi = phi(i) * 2.5
       Else
       kspbphi = 0
       End If

       If phi(i) > 0 Then
       ksnbphi = 0
       ElseIf phi(i) > -0.4 Then
       ksnbphi = -phi(i) * 2.5
       Else
       ksnbphi = 1
       End If

       If phi(i) > 0.1 Then
       kspsphi = 0
       ElseIf phi(i) > 0.05 Then
       kspsphi = 1 - (phi(i) - 0.05) / 0.05
       ElseIf phi(i) > 0 Then
       kspsphi = phi(i) / 0.05
       Else
       kspsphi = 0
       End If

       If phi(i) > 0 Then
       ksnsphi = 0
       ElseIf phi(i) > -0.05 Then
       ksnsphi = -phi(i) / 0.05
       ElseIf phi(i) > -0.1 Then
       ksnsphi = (phi(i) + 0.1) / 0.05
       Else
       ksnsphi = 1
       End If

       If phi(i) > 0.2 Then
       kszophi = 0
       ElseIf phi(i) > 0 Then
       kszophi = 1 - phi(i) * 5
       ElseIf phi(i) > -0.2 Then
       kszophi = 1 + phi(i) * 5
       Else
       kszophi = 0
       End If

       If dphidt(i) > 4 Then
       kszodphi = 0
       kspdphi = 1
       ksndphi = 0
       kspbdphi = 1
       ksnbdphi = 0
       ElseIf dphidt(i) > 0 Then
       kszodphi = 1 - dphidt(i) / 4
       kspdphi = 1
       ksndphi = 1 - dphidt(i) / 4
       kspbdphi = dphidt(i) / 4
       ksnbdphi = 0
       ElseIf dphidt(i) > -4 Then
       kszodphi = 1 + dphidt(i) / 4
       kspdphi = 1 + dphidt(i) / 4
       ksndphi = 1
       kspbdphi = 0
       ksnbdphi = -dphidt(i) / 4
       Else
       kszodphi = 0
       kspdphi = 0
       ksndphi = 1
       kspbdphi = 0
       ksnbdphi = 1
       End If

       kar1 = kspbphi
       If kar1 > kspdphi Then
       kar1 = kspdphi
       End If
       kar2 = ksnbphi
       If kar2 > ksndphi Then
       kar2 = ksndphi
       End If
       kar3 = kspsphi
       If kar3 > ksnbdphi Then
       kar3 = ksnbdphi
       End If
       kar4 = ksnsphi
       If kar4 > kspbdphi Then
       kar4 = kspbdphi
       End If
       kar5 = kspsphi
       If kar5 > kszodphi Then
       kar5 = kszodphi
       End If
       kar6 = ksnsphi
       If kar6 > kszodphi Then
       kar6 = kszodphi
       End If
       dum = kar1 + kar2 + kar3 + kar4 + kar5 + kar6
       If dum > 0 Then
       u(i) = (10 * kar1 - 10 * kar2 - 3 * kar3 + 3 * kar4 + kar5 - kar6) / dum
       Else
       u(i) = 0
       End If
Next

Cells(1, 2) = "時刻t(sec)"
Cells(2, 3) = "y(t)"
Cells(2, 4) = "Φ(t)"
Cells(2, 5) = "u(t)"
Cells(2, 6) = "dy(t)/dt"
Cells(2, 7) = "dΦ(t)/dt"
For i = 0 To 1000
Cells(3 + i, 2) = time(i)
Cells(3 + i, 3) = y(i)
Cells(3 + i, 4) = phi(i)
Cells(3 + i, 5) = u(i)
Cells(3 + i, 6) = dydt(i)
Cells(3 + i, 7) = dphidt(i)
Next

    Range("B2:D1003").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet4").Range("B2:D1003"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet4"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "振子の倒立制御（ファジィ制御）"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = True
        .Axes(xlValue, xlPrimary).AxisTitle.Characters.Text = "y(t)[m],Φ(t)[rad]"
    End With

End Sub

（注）　m-adachi@02.246.ne.jp   へメールで依頼があれば、上記エクセルのソフトをメールの添付ファイルで送ります。

数値シミュレーションの最初のページへ

簡単な常微分方程式の解を求めるシミュレーションへ

ホームページのトップへ