倒立振子のシミュレーション３

　　　　ここでは、振子の振り上げ＋レギュレーション制御を実現する制御手法について紹介する。初期の振子の状態は、真下に自然に垂れ下がっており、台車は原点で静止している場合を扱うものとする。（φ(0)=3.14,dφ(t)/dt=0,y(0)=0,dy(0)/dt=0）

１）振子の振り上げは、台車を前後に動かすことで実現し（剣玉のイメージ）、
２）振子が直立に近くなったら、オブザーバ利用のFB制御（シミュレーション２で用いたもの）でレギュレーションを行う
というシーケンス制御（決まった順番で操作する制御の名称）を使うことを考えてみよう。

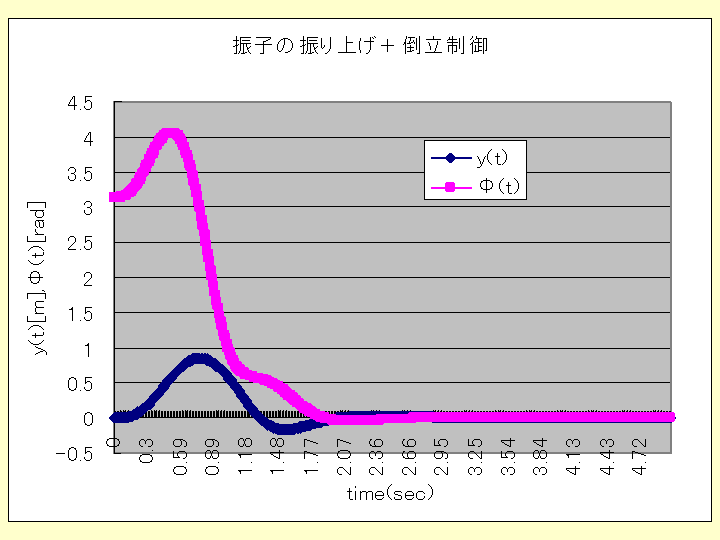
このときの、応答グラフは以下であり、そのソフトはグラフの下に示すものである。ただし、シーケンス制御の最初の台車を前後に動かす操作量としては、
u(t) = 3 * Sin(5 * t)
を用いており、初めて傾き角が０．９[rad]以内に入ってから、オブザーバFB制御に切り替えている。

Sub touritsu7()

Dim A(1 To 2, 1 To 2) As Double, Ainv(1 To 2, 1 To 2) As Double
Dim b(1 To 2, 1 To 2) As Double, dummy(1 To 2) As Double
Dim time(1001) As Double, dt As Double
Dim y(1001) As Double, dydt(1001) As Double, ddyddt(1001)
Dim phi(1001) As Double, dphidt(1001) As Double, ddphiddt(1001)
Dim u(1001) As Double
Dim mp As Double, mc As Double, lambda As Double, ny As Double
Dim leng As Double, inam As Double, ga As Double, g As Double
Dim i As Integer, j As Integer, flag As Integer
Dim ey(1001) As Double, edydt(1001) As Double, eddyddt(1001)
Dim ephi(1001) As Double, edphidt(1001) As Double, eddphiddt(1001)
Dim f(1 To 4) As Double, k(1 To 4, 1 To 2) As Double
Dim AA(1 To 4, 1 To 4) As Double, AAkc(1 To 4, 1 To 4) As Double
Dim delta As Double, bb(1 To 4) As Double, c(1 To 2, 1 To 4) As Double
Dim dum(1 To 4) As Double

   Set WS = Worksheets("Sheet6")
   WS.Activate
   Range("A1:I1300").Select
   Selection.Clear

mp = 0.004735
mc = 0.628
lambda = 0.0001003
ny = 4.01
leng = 0.2465
inam = 0.0001155
ga = 3.18
g = 9.8

flag = 1 ' １：sin入力、２：オブザーバＦＢ制御

' 非線形システムの応答シミュレーション
' 差分時間     0.005
dt = 0.005
For i = 0 To 1000
time(i) = i * dt
u(i) = 0
Next
' 初期値
phi(0) = 3.14
dphidt(0) = 0
y(0) = 0
dydt(0) = 0
ddphiddt(0) = 0
ddyddt(0) = 0

ephi(0) = 3.14
edphidt(0) = 0
ey(0) = 0
edydt(0) = 0

' 近似線形システム
delta = (mp + mc) * inam + mp * mc * leng * leng
AA(1, 1) = 0
AA(1, 2) = 0
AA(1, 3) = 1
AA(1, 4) = 0
AA(2, 1) = 0
AA(2, 2) = 0
AA(2, 3) = 0
AA(2, 4) = 1
AA(3, 1) = 0
AA(3, 2) = -(mp * mp * leng * leng * g) / delta
AA(3, 3) = -ny * (inam + mp * leng * leng) / delta
AA(3, 4) = mp * leng * lambda / delta
AA(4, 1) = 0
AA(4, 2) = mp * leng * (mp + mc) * g / delta
AA(4, 3) = mp * leng * ny / delta
AA(4, 4) = -lambda * (mp + mc) / delta
bb(1) = 0
bb(2) = 0
bb(3) = (inam + mp * leng * leng) * ga / delta
bb(4) = -mp * leng * ga / delta
c(1, 1) = 1
c(1, 2) = 0
c(1, 3) = 0
c(1, 4) = 0
c(2, 1) = 0
c(2, 2) = 1
c(2, 3) = 0
c(2, 4) = 0

' フィードバックゲインf、オブザーバゲインk
f(1) = -10
f(2) = -26.2928
f(3) = -8.4844
f(4) = -4.5618
k(1, 1) = 12.9799
k(2, 1) = 11.1386
k(3, 1) = 9.4331
k(4, 1) = 158.7787
k(1, 2) = 0.2396
k(2, 2) = 22.4001
k(3, 2) = 0.9293
k(4, 2) = 154.2044

For i = 1 To 4
     For j = 1 To 4
     AAkc(i, j) = AA(i, j) - k(i, 1) * c(1, j) - k(i, 2) * c(2, j)
     Next
Next

For i = 1 To 1000
   phi(i) = phi(i - 1) + dphidt(i - 1) * dt
   y(i) = y(i - 1) + dydt(i - 1) * dt

   dphidt(i) = dphidt(i - 1) + ddphiddt(i - 1) * dt
   dydt(i) = dydt(i - 1) + ddyddt(i - 1) * dt

   A(1, 1) = mp + mc
   A(1, 2) = mp * leng * Cos(phi(i - 1))
   A(2, 1) = mp * leng * Cos(phi(i - 1))
   A(2, 2) = inam + mp * leng * leng
   Ainv(1, 1) = A(2, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 2) = A(1, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(1, 2) = -A(1, 2) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))
   Ainv(2, 1) = -A(2, 1) / (A(1, 1) * A(2, 2) - A(1, 2) * A(2, 1))

dummy(1) = Ainv(1, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(1, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(1, 1) * ga * u(i - 1)
dummy(2) = Ainv(2, 1) * (mp * leng * Sin(phi(i - 1)) * dphidt(i - 1) * dphidt(i - 1) - ny * dydt(i - 1)) + Ainv(2, 2) * (-lambda * dphidt(i - 1) + mp * leng * g * Sin(phi(i - 1))) + Ainv(2, 1) * ga * u(i - 1)
ddyddt(i) = dummy(1)
ddphiddt(i) = dummy(2)

Cells(3 + i, 12) = Ainv(1, 1)
Cells(3 + i, 13) = Ainv(1, 2)
Cells(3 + i, 14) = Ainv(2, 1)
Cells(3 + i, 15) = Ainv(2, 2)

If flag = 2 Then
     For j = 1 To 4
     dum(j) = AAkc(j, 1) * ey(i - 1) + AAkc(j, 2) * ephi(i - 1) + AAkc(j, 3) * edydt(i - 1) + AAkc(j, 4) * edphidt(i - 1)
     Next
     ey(i) = ey(i - 1) + (dum(1) + k(1, 1) * y(i - 1) + k(1, 2) * phi(i - 1) + bb(1) * u(i - 1)) * dt
     ephi(i) = ephi(i - 1) + (dum(2) + k(2, 1) * y(i - 1) + k(2, 2) * phi(i - 1) + bb(2) * u(i - 1)) * dt
     edydt(i) = edydt(i - 1) + (dum(3) + k(3, 1) * y(i - 1) + k(3, 2) * phi(i - 1) + bb(3) * u(i - 1)) * dt
     edphidt(i) = edphidt(i - 1) + (dum(4) + k(4, 1) * y(i - 1) + k(4, 2) * phi(i - 1) + bb(4) * u(i - 1)) * dt
u(i) = -f(1) * ey(i) - f(2) * ephi(i) - f(3) * edydt(i) - f(4) * edphidt(i)
'ElseIf flag = 1 And phi(i) < 0.5 And phi(i) > -0.5 Then
'ElseIf flag = 1 And phi(i) < 0.3 And phi(i) > -0.3 Then
'ElseIf flag = 1 And phi(i) < 0.7 And phi(i) > -0.7 Then
ElseIf flag = 1 And phi(i) < 0.9 And phi(i) > -0.9 Then
flag = 2
u(i) = 3 * Sin(5 * i * dt)
ey(i) = y(i)
ephi(i) = phi(i)
edydt(i) = (y(i) - y(i - 1)) / dt
edphidt(i) = (phi(i) - phi(i - 1)) / dt
Else
u(i) = 3 * Sin(5 * i * dt)
End If
Next

Cells(1, 2) = "時刻t(sec)"
Cells(2, 3) = "y(t)"
Cells(2, 4) = "Φ(t)"
Cells(2, 5) = "u(t)"
Cells(2, 6) = "dy(t)/dt"
Cells(2, 7) = "dΦ(t)/dt"

For i = 0 To 1000
Cells(3 + i, 2) = time(i)
Cells(3 + i, 3) = y(i)
Cells(3 + i, 4) = phi(i)
Cells(3 + i, 5) = u(i)
Cells(3 + i, 6) = dydt(i)
Cells(3 + i, 7) = dphidt(i)
Next

    Range("B2:D1003").Select
    Charts.Add
    ActiveChart.ChartType = xlLineMarkers
    ActiveChart.SetSourceData Source:=Sheets("Sheet6").Range("B2:D1003"), PlotBy _
        :=xlColumns
    ActiveChart.Location Where:=xlLocationAsObject, Name:="Sheet6"
    With ActiveChart
        .HasTitle = True
        .ChartTitle.Characters.Text = "振子の振り上げ＋倒立制御"
        .Axes(xlCategory, xlPrimary).HasTitle = True
        .Axes(xlCategory, xlPrimary).AxisTitle.Characters.Text = "time(sec)"
        .Axes(xlValue, xlPrimary).HasTitle = True
        .Axes(xlValue, xlPrimary).AxisTitle.Characters.Text = "y(t)[m],Φ(t)[rad]"
    End With

End Sub

（注）　m-adachi@02.246.ne.jp   へメールで依頼があれば、上記エクセルのソフトをメールの添付ファイルで送ります。

数値シミュレーションの最初のページへ

簡単な常微分方程式の解を求めるシミュレーションへ

ホームページのトップへ