エクセルの基本操作の紹介
まずは、簡単な線形常微分方程式(下記)の解を求めることを通して、微分方程式の解を得るためのエクセルの使い方を紹介します。
dx(t)/dt =- 2*x(t) + u(t), u(t) =
sin(3*t), x(0) = 0
手順1: Microsoft Excel を開く
手順2:
「ツール」 「マクロ」 「Visual Basic Editor」を選択し、「Visual Basic Editor」を開く。
手順3:
そこで、「標準モジュールのModule1」を開く。
手順4:
「標準モジュールのModule1」の中に、実行させたい処理のプログラムを以下のように書く。
Sub sim1()
Dim x(1001) As
Double
Dim u(1001) As
Double
Dim time(1001)
As Double
Dim dt As Double
Dim i As Integer
Set WS =
Worksheets("Sheet1")
WS.Activate
Range("A1:I1300").Select
Selection.Clear
Cells(1, 2) =
"時刻t(sec)"
Cells(2, 3) =
"x(t)"
time(0) = 0
dt = 0.01
x(0) = 0
u(0) = 0
For i = 1 To 1000
time(i) = i * dt
u(i) = Sin(3 * i
* dt)
Next
For i = 1 To 1000
x(i) = x(i - 1)
+ ( - 2 * x(i - 1)+u(i-1)) * dt
Next
For i = 0 To 1000
Cells(3 + i, 2)
= time(i)
Cells(3 + i, 3)
= x(i)
Next
End Sub
手順5:
「標準モジュールのModule1」を開いた状態で、「実行」 「Sub/ユーザーフォームの実行」を選択して、プログラムを実行させる。
手順6:sheet1 に以下のような計算結果が出力されているので、結果を確認する。
| 時刻t(sec) |
|
x(t) |
| 0 |
0 |
| 0.01 |
0 |
| 0.02 |
0.0002 |
| 0.03 |
0.000596 |
| 0.04 |
0.001184 |
| 0.05 |
0.001959 |
| 0.06 |
0.002918 |
| 0.07 |
0.004057 |
| 0.08 |
0.005371 |
| 0.09 |
0.006857 |
| 0.1 |
0.00851 |
| 0.11 |
0.010327 |
| 0.12 |
0.012302 |
| 0.13 |
0.014433 |
| 0.14 |
0.016716 |
| 0.15 |
0.019145 |
| 0.16 |
0.021717 |
| 0.17 |
0.024428 |
| 0.18 |
0.027275 |
| 0.19 |
0.030252 |
| 0.2 |
0.033356 |
| 0.21 |
0.036583 |
| 0.22 |
0.039929 |
| 0.23 |
0.04339 |
| 0.24 |
0.046962 |
| 0.25 |
0.05064 |
| 0.26 |
0.054422 |
| 0.27 |
0.058302 |
| 0.28 |
0.062277 |
・
・
・
・
(注) 微分方程式の定義より、dx(t)/dt =- 2*x(t) + u(t), は、微小な dt に対し、
x(t+dt) = x(t) + [ -2*x(t) + u(t) ]*dt
が成り立つことを意味している。よって、上式を時間発展的に、初期状態 x(0) = 0 から計算して、
x(t) を求めるという、簡易な計算方法を取ることとする。この方法で、気をつけなければならないことは、 dt を微小に取ることである。(dt を
一桁小さくしても計算結果がほとんど変わらなければ、その dt で十分微小であると判断できる。)
さらに、上で得た計算結果をグラフ表示したい場合には、手順4のソフトの End
Sub の前に以下のプログラムを書き入れて手順5、で実行させると、sheet1 に以下のようなグラフを出力させることができる。
Range("B2:C1003").Select
Charts.Add
ActiveChart.ChartType = xlLineMarkers
ActiveChart.SetSourceData
Source:=Sheets("Sheet1").Range("B2:C1003"), PlotBy _
:=xlColumns
ActiveChart.Location Where:=xlLocationAsObject,
Name:="Sheet1"
With ActiveChart
.HasTitle = False
.Axes(xlCategory,
xlPrimary).HasTitle = True
.Axes(xlCategory,
xlPrimary).AxisTitle.Characters.Text = "time(sec)"
.Axes(xlValue,
xlPrimary).HasTitle = False
End With
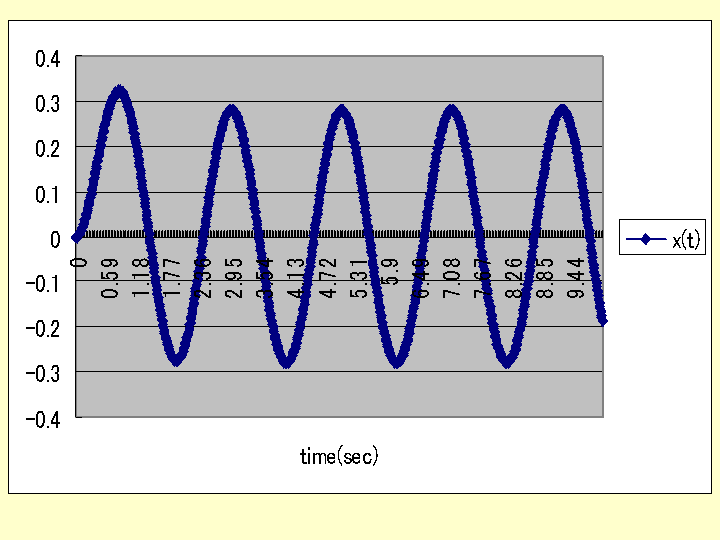
(注)上記微分方程式系の場合、解析解は、 x(t)=3*exp(-2*t)/13 -3*cos(3*t)/13
+2*sin(3*t)/13 であり、解析解とシミュレーション解の相違を調べてみると、差の絶対値の最大値は 0.0035
であり、こんな簡単なシミュレーションで十分な精度の解が得られていることが確かめられる。
さらに、グラフ化の上記ソフトの
.HasTitle = False
の部分を
.HasTitle = True
.ChartTitle.Characters.Text
= "応答波形"
で置き換えると、グラフにタイトル「応答波形」を付けることができる。
また、グラフ化の上記ソフトの
.Axes(xlValue,
xlPrimary).HasTitle = False
の部分を
.Axes(xlValue,
xlPrimary).HasTitle = True
.Axes(xlValue,
xlPrimary).AxisTitle.Characters.Text = "x(t)"
で置き換えると、グラフの縦軸の変数 x(t) を表示させることができる。
(注) m-adachi@02.246.ne.jp
へメールで依頼があれば、上記エクセルのソフトをメールの添付ファイルで送ります。
数値シミュレーションの最初のページへ
簡単な常微分方程式の解を求めるシミュレーションへ
ホームページのトップへ
