実験 3
| 実験前の学習
伝達関数 :
|
この実験では、多目的な制御性能評価を良くする制御の設計について考える。ここでは、DCモータのパラメータ変動や外乱の無い場合の制御問題を扱う。また、用いる制御則は、偏差のフィードバック制御(すなわち、閉ループ制御)のみとする。
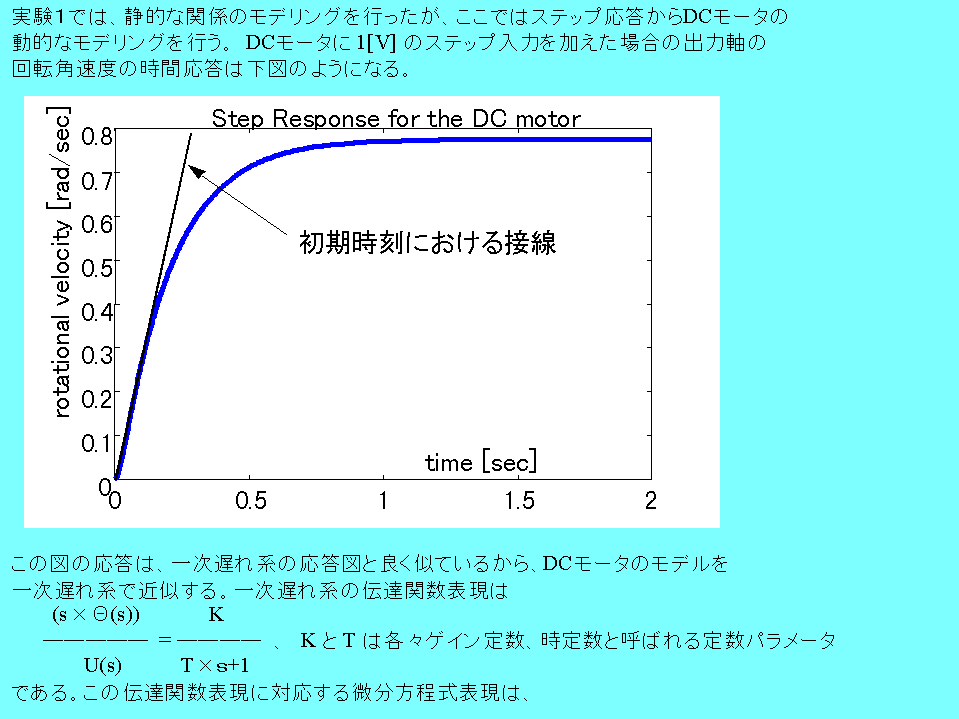
[作業1(モデリング)] ステップ応答法による一次遅れ系のモデリング

d2θ(t)/dt2 = -(1/T)×dθ(t)/dt + (K/T)×u(t)
である。モデルのパラメータである K と T はステップ応答の初期時刻の角速度の傾きと角速度の定常値との間で、
K/T = 初期時刻の角速度の傾き、 K=角速度の定常値
の関係がある。上記応答図から、初期時刻の角速度の傾き=3.1, 角速度の定常値=0.78 と読み取れるから、K=0.78, T=0.78/3.1≒0.25 を得る。
よって、DCモータの動特性の一次遅れモデル :
0.78
――――― を得る。
0.25s+1
[作業2(制御設計)] 極配置によるPI(比例積分)制御の設計
実験2の結果において、比例制御だと定常偏差が残った。定常偏差を除くために良く用いられる手段は、積分制御を付加することである。そこで、PI(比例積分)制御
u(t)=Kp×e(t)+Ki×∫e(t)dt、 ただし、Kp、Ki は定数
を採用してみよう。上式のラプラス変換は、U(s) = ( Kp+
Ki/s )×E(s)、 となる。ただし、U(s)、E(s)は各々 u(t),e(t) のラプラス変換である。e(t)
= r(t) - dθ(t)/dt
モータの伝達関数モデルと上の比例・積分制御より、目標を入力、回転速度を出力とする伝達関数は、
s×Θ(s)
[(s×Θ(s))/U(s)]×(U(s)/E(s))
―――― = ―――――――――――――――、 ただし、R(s)、Θ(s)
は各々、r(t) 、θ(t)のラブラス変換である。
R(s) 1+[(s×Θ(s))/U(s)]×(U(s)/E(s))
より、
s×Θ(s)
K×Kp×s +K×Ki
―――― = ――――――――――――
R(s) T×s2+(1+K×Kp)s +K×Ki
となる。この式の分母=0と置いた式は、この制御系の特性方程式とよばれる。特性方程式の根は、極とよばれる。極の値は、系の応答と深く関係するので、極を指定することにより制御系が設計されることがある。これを、極配置による制御系設計とよばれる。
極配置による閉ループ制御(PI制御)の設計:
極をαとβにしたいとき、T×s2+(1+K×Kp)s +K×Ki = T×(s-α)×(s-β) より、
Kp=[-T×(α+β)-1]/K, Ki=T×α×β/K, でもとめられる比例ゲインKp と積分ゲインKi を使えばよい。
(注) α =- a+b×i、 β= -a-b×i、a>0 , b≧0、i :純虚数、という極の場合、(s-α)(s-β)=(s+a+b×i)(s+a-b×i)=s2+2a×s
+a2+b2
より、固有角周波数は (a2+b2) の平方根、減衰係数は、a/(
(a2+b2) の平方根) となる。したがって、 (a2+b2) の値が大きいときは応答が速くなり、
a にくらべて b が大きいときは、応答において振動が大きくなる。
例えば、 α =- 30+5i、 β= -30-5i
α =-10 、 β=-15
α =-15+15i、 β=-15-15i
α = -30+36i、 β=-30-36i
の4ケースの極配置制御を行う。各ケースの比例ゲイン、積分ゲイン、固有角周波数、減衰係数は下表のようになる。
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Transfer function:
10.93 s + 183.9
-----------------------------------------
0.0039 s^3 + 0.2132 s^2 + 11.93 s + 183.9
Transfer function:
11 s + 185
--------------------
0.2 s^2 + 12 s + 185
Transfer function:
3.975 s + 29.82
-----------------------------------------
0.0039 s^3 + 0.2132 s^2 + 4.975 s + 29.82
Transfer function:
4 s + 30
------------------
0.2 s^2 + 5 s + 30
% ω=sqrt(15*15+15*15)=21.2132 ζ=15/sqrt(15*15+15*15)=
0.7071
Transfer function:
4.969 s + 89.45
-----------------------------------------
0.0039 s^3 + 0.2132 s^2 + 5.969 s + 89.45
Transfer function:
5 s + 90
------------------
0.2 s^2 + 6 s + 90
Transfer function:
10.93 s + 436.5
-----------------------------------------
0.0039 s^3 + 0.2132 s^2 + 11.93 s + 436.5
Transfer function:
11 s + 439.2
----------------------
0.2 s^2 + 12 s + 439.2
[作業3(性能評価)] ステップ応答による評価
極をかえた場合の制御応答を比べてみよう。目標速度を 1 [rad/sec] の単位ステップ関数(r(t)=0, for t<0, r(t)=1, for t≧0)とした場合に、PI制御則の比例・積分ゲインを作業2で求めたつ4ケースの値 Kp=14.1 ,Ki=237 、Kp=5.1 ,Ki= 38.5、Kp=6.4 ,Ki=115、Kp=14.1 ,Ki=563、で与えた場合のステップ応答と操作量のグラフを以下に示す。
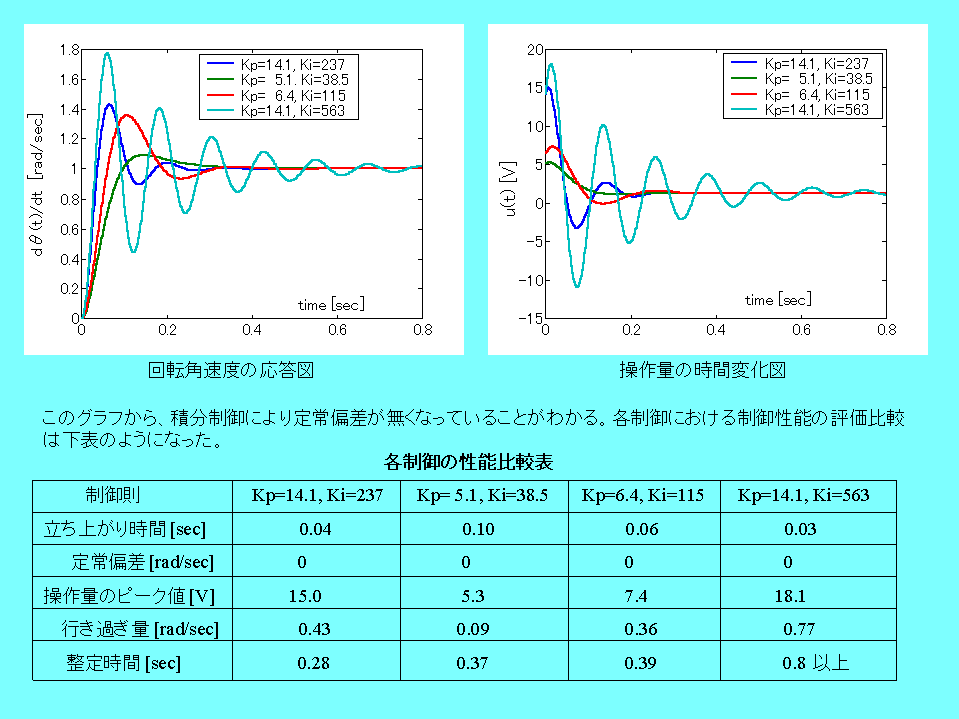
(注)整定時間とは、その時間以後は応答が目標値の近傍にとどまるとき、その条件を満たす最小の時刻をいう。この時間は、近傍の定義依存であり、ここでは、1±0.01 [rad/sec] の範囲としている。
上記の表の結果より、次のようなことが分かる。
1) 固有角周波数を大きくすると立ち上がりが速くなる。
2) 積分制御で定常偏差が0となる。
3) 減衰係数が小さいと、行き過ぎ量は大きくなり、整定時間は長くなる。(ただし、Kp=6.4,
Ki=115 の場合は例外か?)
[作業4(性能評価)] 目標が周期関数である場合(このような制御をトラッキング制御という)の評価
いままでの実験における目標は一定な回転速度(ステップ関数)であったが、この作業においては、目標を周期関数 sin(10πt) とする。目標関数が時間に依存するものに変わった場合について、作業3の4ケースの制御がどのような制御性能を示すのか調べてみよう。実験結果の最初の 0.4 秒間(過渡応答)と、1.6 秒から 2.0 秒までの 0.4 秒間(ほぼ繰り返しの周期関数のみの応答)について、速度と操作量の時間変化を示したものが下のグラフである。
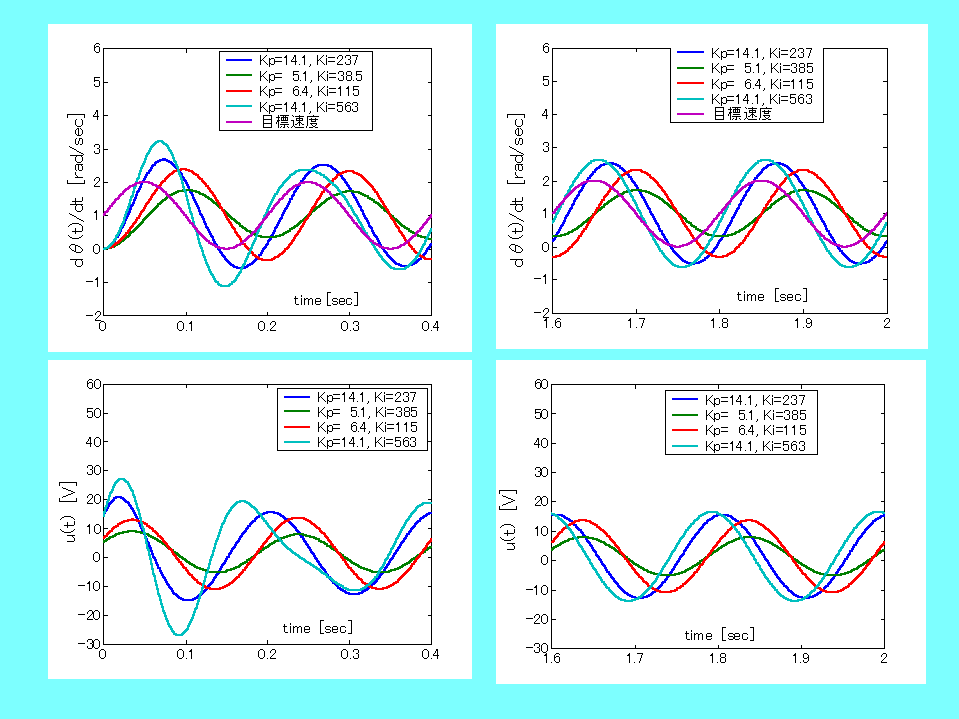
ステップ応答と異なり、このような目標に対する応答は周波数応答とよばれ、制御性能は振幅比や位相差で測られる。
|
|
|
|
|
Kp=14.1 ,Ki= 563 |
|
|
|
|
|
|
|
|
|
|
|
|
(注)振幅比、位相差の説明 : 線形システムに周期関数(例えば、sin(ωt) を入力すると、過渡的には乱れた応答波形となるが、十分時間が経って過渡的なものが消えると、応答波形は a×sin(ωt+b) となる。この a は振幅比、b は位相差と呼ばれる。
上記の結果から、目標が周期関数であるトラッキング制御問題の場合には、目標がステップ関数に対するものとは異なる制御則を設計する必要があることが分かる。
[作業5(モデリング)] ステップ応答法による二次遅れ系のモデリング
実験2作業1の比例制御 u(t)=12.9×e(t) をした時のステップ応答図から、DCモータの電圧を入力、回転角速度を出力とする、モデルは一次遅れ系ではなく、二次以上の遅れ系であることがわかる。
(なぜなら、一次遅れ系 s×Θ(s)/U(s)=K/(T×s+1) に対し比例の偏差フィードバック制御
U(s)=Kp×[R(s)-s×Θ(s)] しても閉ループ系の伝達関数は s×Θ(s)/R(s)=K×Kp/(T×s+1+K×Kp)
となり、一次遅れ系のままで変わらず、よって、行き過ぎ量は存在しない。しかし、実験2の応答図では、行き過ぎ量が発生している。)
二次遅れ系でDCモータを近似しよう。 二次遅れ系の伝達関数表現は、
s×Θ(s)
K
―――― = ――――――――――――
U(s) s2/ω2+2ζ×s/ω+1
K 、 ω、ζ は各々、ゲイン定数、固有角周波数、減衰係数と呼ばれる定数パラメータである。この伝達関数表現に対応する微分方程式表現は、
d3θ(t)
d2θ(t)
dθ(t)
―――― = -2ζ×ω×――――
- ω2×――― + K×ω2×u(t)
dt3
dt2
dt
である。この系に対し、 u(t)=12.9×e(t) (すなわち、U(s)=12.9×[R(s)-s×Θ(s)
]) の比例フィードバック制御を行うと、伝達関数は
s×Θ(s)
12.9×K
―――― = ――――――――――――
R(s) s2/ω2+2ζ×s/ω+1+12.9×
K
となる。この二次遅れ系のゲイン定数、固有角周波数、減衰係数 を、各々、 newK、 newω、 newζ で表現すると、
newK = 12.9× K/(1+12.9× K)、
(1)
newω= (12.9× K×ω2)の平方根、
(2)
newζ= ζ/((12.9× K×ω2)の平方根)
(3)
の関係が成り立つ。実験2の比例制御時のステップ応答より、定常値は
0.91 [rad/sec] と計測されたので、
newK = 12.9× K/(1+12.9× K)
= 0.91
(A)
また、応答図よりステップ応答のピークタイム、行き過ぎ量はそれぞれ、0.068
[sec], 0.14 [rad/sec] と計測されたので、
π/[(1-newζ*newζ)の平方根*newω] = 0.068
(B)
[ 12.9*K/(1+12.9*K)]*exp{-π*newζ/[(1-newζ*newζ)の平方根]}=
0.14
(C)
の関係式を得る。式 (A)、(B)、 (C)を解いて、newK =
0.91、newω= 53.6、newζ=0.51 を得る。この値を式(1)、 (2)、 (3) に代入して、連立方程式を解くと、K=0.78、ω=
16.2、ζ= 1.70 を得る。これらの値を二次遅れ系の伝達関数に代入し次のモデルが導かれる。
s×Θ(s)
0.78
―――― = ――――――――――――
U(s) 0.0038×s2+0.21×s+1
[作業6(考察)]
目標が周期関数の場合、実験2の場合は、閉ループ+開ループ制御で追従することができたが、実験3では追従できていない。 これは、何を意味するのであろうか? 開ループ制御も実験2では行ったが、実験3では閉ループ制御のみということも理由の候補として考えられる。 しかし、はっきり言えることは、目標が時間的に非常にゆっくり変わるとき(すなわち、目標の周期関数の周期が振幅に比べて長いとき)、ステップ応答に追従するように設計された制御で、周期目標に追従できるということとの関係である。 実験2での目標関数の周期は1秒に対し、実験3での周期は0.2秒ということが一つの原因であることは明らかである。
一次遅れモデルの限界
実験室3では、ダイナミックスのモデリングと補償器を紹介する。実験室1の時と同じように、モデリングを最初に行う。一次遅れ系モデル、比例・積分(PI)型制御器を使うことで、モデルの複雑さと目標仕様は高度になる。モデルの複雑さは、設計者が選択するものである。
一次遅れモデルは、オープンループのステップ応答の立ち上がり時間と振幅情報を用いて決める。実験室1のモデリングのための計測は速度の定常応答に関してであったが、実験室3では、過渡応答値を用いている。PI型補償器(設計パラメータは2個)を用いると、トータルのシステムは二次遅れ系となる。極配置法で補償器を設計する。一次遅れ系モデルの限界を明らかにする。制御系の構造は図4に示すものである。周期入力信号に対する偏差応答を調べる、これが次の実験室における周波数応答によるモデリングの準備となる。